Retém a instrução e não a largues. guarda-a, porque ela é a tua vida. (Pv. 4:13)
Retém a instrução e não a largues. Guarda-a, porque ela é a tua vida. (Pv. 4:13)
Mostrando postagens com marcador 9º ANO 8ª SÉRIE. Mostrar todas as postagens
Mostrando postagens com marcador 9º ANO 8ª SÉRIE. Mostrar todas as postagens
19 de maio de 2011
TEOREMA DE PITÁGORAS
A HIPOTENUSA MALDITA
4 de maio de 2011
9º ANO 8ª SÉRIE
GRÁFICOS ESTATÍSTICOS
Os gráficos constituem uma forma clara e objetiva na apresentação de dados estatísticos,
a intenção é de proporcionar aos leitores em geral a compreensão e veracidade dos fatos.
De acordo com a característica da informação precisamos escolher o gráfico correto,
os mais usuais são: gráfico de segmentos, gráfico de barras e gráfico de setores.
Gráfico de Segmento ou gráfico de linhas
Objetivos: simplicidade, clareza e veracidade.
a intenção é de proporcionar aos leitores em geral a compreensão e veracidade dos fatos.
De acordo com a característica da informação precisamos escolher o gráfico correto,
os mais usuais são: gráfico de segmentos, gráfico de barras e gráfico de setores.
Gráfico de Segmento ou gráfico de linhas
Objetivos: simplicidade, clareza e veracidade.
Uma locadora de filmes em DVD registrou o número de locações no 1º semestre do ano de 2008.
Os dados foram expressos em um gráfico de segmentos.
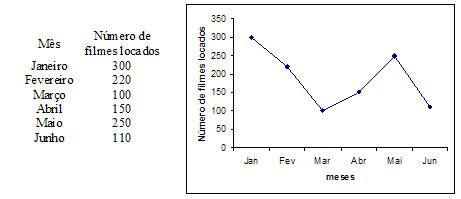
Gráfico de Barras horizontal e vertical
Objetivo: representar os dados através de retângulos, com o intuito de analisar as
projeções no período determinado.
O exemplo abaixo mostra o consumo de energia elétrica no decorrer do ano de
2005 de uma família.
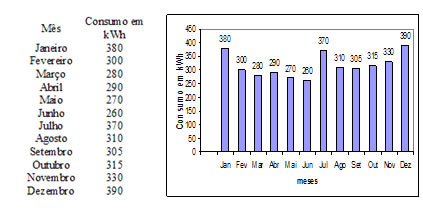
Objetivo: representar os dados através de retângulos, com o intuito de analisar as
projeções no período determinado.
O exemplo abaixo mostra o consumo de energia elétrica no decorrer do ano de
2005 de uma família.


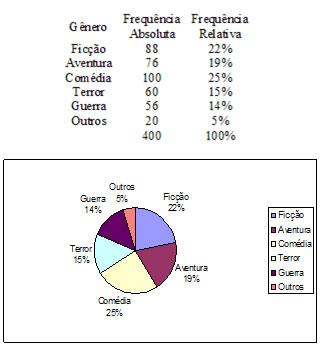
Objetivos: expressar as informações em uma circunferência fracionada. É um gráfico
muito usado na demonstração de dados percentuais.
O gráfico a seguir mostrará a preferência dos clientes de uma locadora quanto ao gênero
dos filmes locados durante a semana.
| OPERAÇÕES COM RADICAIS |
| 14.0 - Adição e Subtração de Radicais |

| 15.0 - Multiplicação de Radicais |

| 16.0 - Divisão de Radicais |

| 17.0 - Potenciação de Radicais |

| 18.0 - Radiciação de Radicais |

| 19.0 - Frações Irracionais |

| 20.0 - Racionalização de Denominadores Irracionais. |
| 20.1 - O denominador é um radical quadrático. |

| 20.2 - O denominador é um radical de índice maior que dois. |

| 20.3 - O denominador é uma expressão irracional contendo pelo menos um radical quadrático. |

| 21.0 - Exercícios Resolvidos - Parte II |

EQUAÇÃO DO 2° GRAU
A fórmula quadrática de Sridhara (Bhaskara)
Mostraremos na sequência como o matemático Sridhara, obteve a Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula geral para a resolução de equações do segundo grau. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.
O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.
Seja a equação:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0
2) 3 x² + x + 2 = 0
o coeficiente a é diferente de zero.
Exemplos:
1) 4 x² + 6x = 0
2) 3 x² + 9 = 0
3) 2 x² = 0
Resolução de equações completas do 2° grau
Como vimos, uma equação do tipo: ax²+bx+c=0, é uma equação completa do segundo grau e para resolvê-la basta usar a fórmula quadrática (atribuída a Bhaskara), que pode ser escrita na forma:
onde Δ=b²-4ac é o discriminante da equação.Para esse discriminante Δ, há três possíveis situações:
1) Δ <> 0, há duas soluções reais e diferentes
Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:
x² - 5 x + 6 = 0
1) Identificar os coeficientes: a=1, b= -5, c=6
2) Escrever o discriminante Δ = b²-4ac.
3) Calcular Δ=(-5)²-4×1×6=25-24=1
4) Escrever a fórmula de Bhaskara:
EXERCÍCIOS
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:
a) x² + 9 x + 8 = 0 (R:-1 e -8)
b) 9 x² - 24 x + 16 = 0 (R:4/3)
c) x² - 2 x + 4 = 0 (vazio)
d) 3 x² - 15 x + 12 = 0 (R: 1 e 4)
e) 10 x² + 72 x - 64 = 0 (R:-8 e 4/5)
e) 5x² - 3x - 2 = 0
f) x² - 10x + 25 = 0
g) x² - x - 20 = 0
h) x² - 3x -4 = 0
i) x² - 8x + 7 = 0
RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2,)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:3,7)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)
35)Na equação 3x² - 12 = 0 as soluções são:
a)0 e 1
b)-1 e 1
c)-2 e 2 (x)
d)-3 e 3
e)0 e 4
36) x² + 3x - 28 = 0 (R: -7,4)
37) 3x² - 4x + 2 = 0 (R: vazio)
38) x² - 3 = 4x + 2 (R: -1,5)
PROBLEMAS COM EQUAÇÃO DO 2° GRAU
1) A soma de um numero com o seu quadrado é 90. Calcule esse numero. (R:9 e-10)
2) A soma do quadrado de um número com o próprio número é 12. Calcule esse numero (R: 3 e -4)
3) O quadrado menos o dobro de um número é igual a -1. Calcule esse número. (R:1)
4) A diferença entre o quadrado e o dobro de um mesmo número é 80. Calcule esse número (R:10 e -8)
5) O quadrado de um número aumentado de 25 é igual a dez vezes esse número. Calcule esse número (R: 5)
6) A soma do quadrado de um número com o seu triplo é igual a 7 vezes esse número. Calcule esse número.(R: 0 e 4)
7) O quadrado menos o quádruplo de um numero é igual a 5. Calcule esse número (R: 5 e -1)
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero? (R: 6 e -3)
9) O dobro do quadrado de um número é igual ao produto desse numero por 7 menos 3. Qual é esse numero? (R:3 e ½)
10) O quadrado de um número menos o triplo do seu sucessivo é igual a 15. Qual é esse numero?(R: 6 e -3)
11) Qual o número que somado com seu quadrado resulta em 56? (R:-8 e 7)
12) Um numero ao quadrado mais o dobro desse número é igual a 35. Qual é esse número ? (R:-7 e 5)
13) O quadrado de um número menos o seu triplo é igual a 40. Qual é esse número? (R:8 e -5)
14) Calcule um número inteiro tal que três vezes o quadrado desse número menos o dobro desse número seja igual a 40. (R:4)
15) Calcule um número inteiro e positivo tal que seu quadrado menos o dobro desse número seja igual a 48. (R:8)
16) O triplo de um número menos o quadrado desse número é igual a 2. Qual é esse número? (R:1 e 2)
17) Qual é o número , cujo quadrado mais seu triplo é igual a 40? ( R: 5 , -8)
18) O quadrado de um número diminuido de 15 é igual ao seu dobro. Calcule esse número.
(R: 5 e -3)
19) Determine um número tal que seu quadrado diminuído do seu triplo é igual a 26. (R:7 e -4)
20) Se do quadrado de um número, negativo subtraimos 7, o resto será 42. Qual é esse número?
(R: -7)
21) A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número. (R: 7)
22) Determine dois números ímpares consecutivos cujo produto seja 143. (R: 11 e 13 ou -11, -13)
23) Um azulejista usou 2000 azulejos quadrados e iguais para revestir 45m² de parede. Qual é a medida do lado de cada azulejo? (R:15 cm)
RESOLUÇÃO DE EQUAÇÃO INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau
a) x² - 49 = 0 (R: -7 e +7)
b) x² = 1 (R: +1 e -1)
c) 2x² - 50 = 0 (R: 5 e -5)
d) 7x² - 7 = 0 (R: 1 e -1)
e) 5x² - 15 = 0 (R: √3 e -√3)
f) 21 = 7x² (R: √3 e -√3)
g) 5x² + 20 = 0 (R: vazio)
h) 7x² + 2 = 30 (R: 2 e -2 )
i) 2x² - 90 = 8 (R: 7 e -7)
j) 4x² - 27 = x² (R:3 e -3)
k) 8x² = 60 – 7x² (R: 2 e -2)
l) 3(x² - 1 ) = 24 (R: 3 e -3)
m) 2(x² - 1) = x² + 7 (R:3 e -3)
n) 5(x² - 1) = 4(x² + 1) (R:3 e -3)
o) (x – 3)(x + 4) + 8 = x (R:2 e -2)
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
Mostraremos na sequência como o matemático Sridhara, obteve a Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula geral para a resolução de equações do segundo grau. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.
O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.
Seja a equação:
ax² + bx + c = 0
onde os números reais a, b e c são os coeficientes da equação, sendo que a deve ser diferente de zero. Essa equação é também chamada de equação quadrática, pois o termo de maior grau está elevado ao quadrado
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes a, b e c são diferentes de zero.
Exemplos:
1) 2 x² + 7x + 5 = 0
2) 3 x² + x + 2 = 0
o coeficiente a é diferente de zero.
Exemplos:
1) 4 x² + 6x = 0
2) 3 x² + 9 = 0
3) 2 x² = 0
Resolução de equações completas do 2° grau
Como vimos, uma equação do tipo: ax²+bx+c=0, é uma equação completa do segundo grau e para resolvê-la basta usar a fórmula quadrática (atribuída a Bhaskara), que pode ser escrita na forma:
onde Δ=b²-4ac é o discriminante da equação.Para esse discriminante Δ, há três possíveis situações:
1) Δ <> 0, há duas soluções reais e diferentes
Mostraremos agora como usar a fórmula de Bhaskara para resolver a equação:
x² - 5 x + 6 = 0
1) Identificar os coeficientes: a=1, b= -5, c=6
2) Escrever o discriminante Δ = b²-4ac.
3) Calcular Δ=(-5)²-4×1×6=25-24=1
4) Escrever a fórmula de Bhaskara:
EXERCÍCIOS
1. Calcular o discriminante de cada equação e analisar as raízes em cada caso:
a) x² + 9 x + 8 = 0 (R:-1 e -8)
b) 9 x² - 24 x + 16 = 0 (R:4/3)
c) x² - 2 x + 4 = 0 (vazio)
d) 3 x² - 15 x + 12 = 0 (R: 1 e 4)
e) 10 x² + 72 x - 64 = 0 (R:-8 e 4/5)
e) 5x² - 3x - 2 = 0
f) x² - 10x + 25 = 0
g) x² - x - 20 = 0
h) x² - 3x -4 = 0
i) x² - 8x + 7 = 0
RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2,)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:3,7)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)
35)Na equação 3x² - 12 = 0 as soluções são:
a)0 e 1
b)-1 e 1
c)-2 e 2 (x)
d)-3 e 3
e)0 e 4
36) x² + 3x - 28 = 0 (R: -7,4)
37) 3x² - 4x + 2 = 0 (R: vazio)
38) x² - 3 = 4x + 2 (R: -1,5)
PROBLEMAS COM EQUAÇÃO DO 2° GRAU
1) A soma de um numero com o seu quadrado é 90. Calcule esse numero. (R:9 e-10)
2) A soma do quadrado de um número com o próprio número é 12. Calcule esse numero (R: 3 e -4)
3) O quadrado menos o dobro de um número é igual a -1. Calcule esse número. (R:1)
4) A diferença entre o quadrado e o dobro de um mesmo número é 80. Calcule esse número (R:10 e -8)
5) O quadrado de um número aumentado de 25 é igual a dez vezes esse número. Calcule esse número (R: 5)
6) A soma do quadrado de um número com o seu triplo é igual a 7 vezes esse número. Calcule esse número.(R: 0 e 4)
7) O quadrado menos o quádruplo de um numero é igual a 5. Calcule esse número (R: 5 e -1)
8) O quadrado de um número é igual ao produto desse número por 3, mais 18. Qual é esse numero? (R: 6 e -3)
9) O dobro do quadrado de um número é igual ao produto desse numero por 7 menos 3. Qual é esse numero? (R:3 e ½)
10) O quadrado de um número menos o triplo do seu sucessivo é igual a 15. Qual é esse numero?(R: 6 e -3)
11) Qual o número que somado com seu quadrado resulta em 56? (R:-8 e 7)
12) Um numero ao quadrado mais o dobro desse número é igual a 35. Qual é esse número ? (R:-7 e 5)
13) O quadrado de um número menos o seu triplo é igual a 40. Qual é esse número? (R:8 e -5)
14) Calcule um número inteiro tal que três vezes o quadrado desse número menos o dobro desse número seja igual a 40. (R:4)
15) Calcule um número inteiro e positivo tal que seu quadrado menos o dobro desse número seja igual a 48. (R:8)
16) O triplo de um número menos o quadrado desse número é igual a 2. Qual é esse número? (R:1 e 2)
17) Qual é o número , cujo quadrado mais seu triplo é igual a 40? ( R: 5 , -8)
18) O quadrado de um número diminuido de 15 é igual ao seu dobro. Calcule esse número.
(R: 5 e -3)
19) Determine um número tal que seu quadrado diminuído do seu triplo é igual a 26. (R:7 e -4)
20) Se do quadrado de um número, negativo subtraimos 7, o resto será 42. Qual é esse número?
(R: -7)
21) A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número. (R: 7)
22) Determine dois números ímpares consecutivos cujo produto seja 143. (R: 11 e 13 ou -11, -13)
23) Um azulejista usou 2000 azulejos quadrados e iguais para revestir 45m² de parede. Qual é a medida do lado de cada azulejo? (R:15 cm)
RESOLUÇÃO DE EQUAÇÃO INCOMPLETAS
Resolver uma equação é determinar todas as suas soluções. Vejamos, através de exemplos, como se resolvem as equações incompletas do 2° grau
1° CASO – equações da forma ax² + c = 0, (b = 0)
Exemplos:
1) x² - 25 = 0
x² = 25
x = √25
x = 5
logo V= (+5 e -5)
2) 2x² - 18 = 0
2x² = 18
x² = 18/2
x² = 9
x = √9
x = 3
logo V= (-3 e +3)
3) 7x² - 14 = 0
7x² = 14
x² = 14/7
x² = 2
x = √2
logo V = (-√2 e +√2)
4) x²+ 25 = 0
x² = -25
x = √-25
obs: não existe nenhum número real que elevado ao quadrado seja igual a -25
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau
a) x² - 49 = 0 (R: -7 e +7)
b) x² = 1 (R: +1 e -1)
c) 2x² - 50 = 0 (R: 5 e -5)
d) 7x² - 7 = 0 (R: 1 e -1)
e) 5x² - 15 = 0 (R: √3 e -√3)
f) 21 = 7x² (R: √3 e -√3)
g) 5x² + 20 = 0 (R: vazio)
h) 7x² + 2 = 30 (R: 2 e -2 )
i) 2x² - 90 = 8 (R: 7 e -7)
j) 4x² - 27 = x² (R:3 e -3)
k) 8x² = 60 – 7x² (R: 2 e -2)
l) 3(x² - 1 ) = 24 (R: 3 e -3)
m) 2(x² - 1) = x² + 7 (R:3 e -3)
n) 5(x² - 1) = 4(x² + 1) (R:3 e -3)
o) (x – 3)(x + 4) + 8 = x (R:2 e -2)
2° CASO: Equações da forma ax² + bx = 0 ( c = 0)
Propriedade: Para que um produto seja nulo é preciso que um dos fatores seja zero .
Exemplos
1) resolver x² - 5x = 0
fatorando x ( x – 5) = 0
deixando um dos fatores nulo temos x = 0
e o outro x – 5 = 0 , passando o 5 para o outro lado do igual temos x = 5
logo V= (0 e 5)
2) resolver: 3x² - 10x = 0
fatorando: x (3x – 10) = 0
deixando um dos fatores nulo temos x = 0
Tendo também 3x – 10 = 0
3x = 10
x = 10/3
logo V= (0 e 10/3)
Observe que, nesse caso, uma das raízes é sempre zero.
EXERCÍCIOS
1) Resolva as seguintes equações do 2° grau.
a) x² - 7x = 0 (R: 0 e 7)
b) x² + 5x = 0 (R: 0 e -5)
c) 4x² - 9x = 0 (R: 0 e 9/4)
d) 3x² + 5x =0 (R: 0 e -5/3)
e) 4x² - 12x = 0 (R: 0 e 3)
f) 5x² + x = 0 (R: 0 e -1/5)
g) x² + x = 0 (R: 0 e -1)
h) 7x² - x = 0 (R: 0 e 1/7)
i) 2x² = 7x (R: 0 e 7/2)
j) 2x² = 8x (R: 0 e 4)
k) 7x² = -14x (R: 0 e -2)
l) -2x² + 10x = 0 (R: 0 e 5)
2) Resolva as seguintes equações do 2° grau
a) x² + x ( x – 6 ) = 0 (R: 0 e 3)
b) x(x + 3) = 5x (R: 0 e 2)
c) x(x – 3) -2 ( x-3) = 6 (R: 0 e 5)
d) ( x + 5)² = 25 (R: 0 e -10)
e) (x – 2)² = 4 – 9x (R: 0 e -5)
f) (x + 1) (x – 3) = -3 (R: 0 e 2)
EQUAÇÕES FRACIONÁRIAS
Conceito: Uma fração é fracionária quando apresenta variável no denominador.
Exemplos :
a) 5/2x – 8 = 7/x
b) 4x / (x -2) + 5/(x-1) = 6
CONJUNTO UNIVERSO DE UMA EQUAÇÃO FRACIONÁRIA
O denominador nunca pode ser zero.
O conjunto universo de uma equação fracionária não deve conter os valores que anulem o denominador.
RESOLUÇÃO DE EQUAÇÕES FRACIONÁRIAS
As equações fracionárias são resolvidas do mesmo modo que se resolvem as equações que apresentam denominadores numéricos.
EXERCÍCIOS
Conceito: Uma fração é fracionária quando apresenta variável no denominador.
Exemplos :
a) 5/2x – 8 = 7/x
b) 4x / (x -2) + 5/(x-1) = 6
CONJUNTO UNIVERSO DE UMA EQUAÇÃO FRACIONÁRIA
O denominador nunca pode ser zero.
O conjunto universo de uma equação fracionária não deve conter os valores que anulem o denominador.
RESOLUÇÃO DE EQUAÇÕES FRACIONÁRIAS
As equações fracionárias são resolvidas do mesmo modo que se resolvem as equações que apresentam denominadores numéricos.
EXERCÍCIOS
1) Resolva as equações fracionárias
a) 2/x + 1 = 4/x
b) 8 – 5/x = 3/x
c) 10/x – 3 = 5/2
d) 1/x + 1/2 = 5/x
e) 1/x + 3/4 = 5/2x
f) 7/2x + 3 = 8/x
g) (x -2) / x = 2/7
h) (3x – 1)/ x = 5/3
.
.
.
.
.
.
.
.
EXERCÍCIOS
1) Resolva as equações fracionárias
a) 6/ (x + 2) = 3/ (x -8)
b) (x – 1 ) / (x – 2) = (x + 1) / ( x – 1)
c) 12/ (x +3) = 8/ (x -3)
d) X / (x -2) + x / (x + 1) = 2
e) 4/ (x -5) = 2/(2x -3)
f) (x +3)/x = (x +9) / (x + 4)
g) 6/(x +2) = 3/x – 9/x
h) X / (x -1) + 1 (x -1) = 5/3
1) Resolva as equações fracionárias
a) 6/ (x + 2) = 3/ (x -8)
b) (x – 1 ) / (x – 2) = (x + 1) / ( x – 1)
c) 12/ (x +3) = 8/ (x -3)
d) X / (x -2) + x / (x + 1) = 2
e) 4/ (x -5) = 2/(2x -3)
f) (x +3)/x = (x +9) / (x + 4)
g) 6/(x +2) = 3/x – 9/x
h) X / (x -1) + 1 (x -1) = 5/3
.
.
.
.
.
EXERCÍCIOS
1) Resolva as equações fracionarias
a) 2/(x -1) + 1 / (x² -1)= 0
b) x/(x + 3) – 1 = 5 / (x² - 9)
c) 1/ (x -2) + 1/(x+2) = 4/ (x² -4)
d) 2/(x -1) + 3 (x +1) = 4 / (x² - 4)
e) 3/ ( x + 1) – 4/ 3(x -1) = 4/ (x² - 1)
2) Resolva as equações fracionárias
1) Resolva as equações fracionarias
a) 2/(x -1) + 1 / (x² -1)= 0
b) x/(x + 3) – 1 = 5 / (x² - 9)
c) 1/ (x -2) + 1/(x+2) = 4/ (x² -4)
d) 2/(x -1) + 3 (x +1) = 4 / (x² - 4)
e) 3/ ( x + 1) – 4/ 3(x -1) = 4/ (x² - 1)
2) Resolva as equações fracionárias
a) 3/x + 4/9 = 5/12
b) 3/x – 1 = 3/2
c) 2 + 1/x = 7/x
d) 9/x + 6/x = 3
e) 8 – 3/x = 1/x
f) 3/x + ¼ = 2/x
g) 1/2x + 3/8 = 2/x
h) (x +1)/ 3x + 1/x = 2/3
i) 3/4x – 3/5x + 1/10 = 0
j) (4x + 5) / 8x – ¾ = (1 –x) / 2x
k) (x -3) / (x + 3) = 3/5
l) 3x / (x – 4) -2/x = 3
m) (x + 7) / (x + 5) – 12/(x -5) = 1
SISTEMAS SIMPLES DO 2° GRAU
Vamos resolver sistemas que possuem uma equação do 1° grau e outra do 2° grau polo método da substituição .
Exemplo
a)x - y = 1
__x . y = 6
Isolando x na equação x - y = 1, temos x = 1 + y
substituindo esse valor de x em x . y = 6 , obtemos,
(1+ y) . y = 6
y + y² = 6
y² + y - 6 = 0
resolvendo essa equação do 2° grau temos:
solução ( 2 e -3)
b) x + y = 7
___x². y² = 25
Isolando x na equação x + y = 7, temos x = 7 - y
substituindo esse valor de x em x². y² = 25, obtemos
(7 - y)² + y² = 25
49 - 14y + y² + y² = 25
2y² - 14y + 49 - 25 = 0
2y² - 14y + 24 = 0
resolvendo essa equação do 2° grau temos:
solução [(3 e 4) e (4 e 3)]
Exercícios
1) x + y = 7______ (R:2,5 ou 5,2)
x . y = 10
2)x + y = 5______ (R:2,3 ou 3,2)
__x . y = 6
3) x - y = 9______ (R:2,-7 ou -7,2)
x . y = -14
4) x - y = 3______ (R:6,3 ou -3,-6)
x²+ y² = 45
5) x - y = 1______ (R: 4,3 ou -3,-4)
x²+ y² = 25
b) x - y = 0______ (R: 2,2 ou -2,-2)
5x²- y² = 16
Vamos resolver sistemas que possuem uma equação do 1° grau e outra do 2° grau polo método da substituição .
Exemplo
a)x - y = 1
__x . y = 6
Isolando x na equação x - y = 1, temos x = 1 + y
substituindo esse valor de x em x . y = 6 , obtemos,
(1+ y) . y = 6
y + y² = 6
y² + y - 6 = 0
resolvendo essa equação do 2° grau temos:
solução ( 2 e -3)
b) x + y = 7
___x². y² = 25
Isolando x na equação x + y = 7, temos x = 7 - y
substituindo esse valor de x em x². y² = 25, obtemos
(7 - y)² + y² = 25
49 - 14y + y² + y² = 25
2y² - 14y + 49 - 25 = 0
2y² - 14y + 24 = 0
resolvendo essa equação do 2° grau temos:
solução [(3 e 4) e (4 e 3)]
Exercícios
1) x + y = 7______ (R:2,5 ou 5,2)
x . y = 10
2)x + y = 5______ (R:2,3 ou 3,2)
__x . y = 6
3) x - y = 9______ (R:2,-7 ou -7,2)
x . y = -14
4) x - y = 3______ (R:6,3 ou -3,-6)
x²+ y² = 45
5) x - y = 1______ (R: 4,3 ou -3,-4)
x²+ y² = 25
b) x - y = 0______ (R: 2,2 ou -2,-2)
5x²- y² = 16
Assinar:
Postagens (Atom)
